I have removed the Second Skin from my new tattoo, and the itching is absolutely maddening, so I’m going to distract myself with math. Because that’s why you come here, right? As a reminder, this is the original image, and the question is the ratio of the inner square to the outer square:

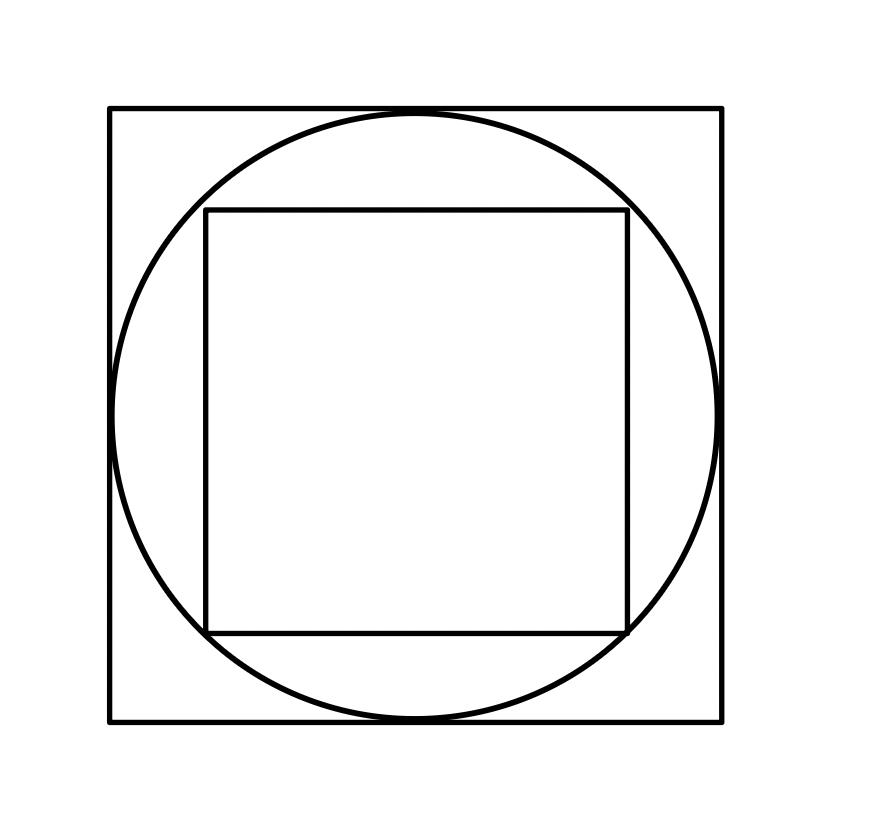
The first thing we’re going to do is draw the two diagonals of the inner square. These are, by definition, perpendicular to each other, and they are also equal to the circumference of the circle. Let us define the radius of the circle as x:

What we have now is four right triangles inscribed inside the circle. Pythagoras tells us that the sum of the squares of the two legs are equal to the square of the hypotenuse, which is the line on the left of the square there. Therefore, defining the hypotenuse as Y, we get:

x² + x² = y²
2x² = y²

Take the square roots of each side, and we get:

√(2x²) = √(y²)

And therefore:

√(2x²) = y

Which means that all four sides of the inner circle are equal to √(2x²), thusly:

To get the area of the inner square, all we have to do is multiply √(2x²) by √(2x²), which, conveniently, just gets rid of the square root symbols. The area of the inner circle is 2x².

Now, we need to realize that since the radius of the circle is x, the diameter of the circle is 2x, and that the diameter of the circle also equals the width and the height of the outside square. So that outer square is 2x high and 2x wide:

Therefore, all we have to do to get the area of the outside square is multiply 2x by 2x, which gives us 4x². Which, conveniently, is exactly twice the area of the inner square, which was 2x².

The outside square is therefore twice the size of the inner square, and the ratio of the inner square to the outer square is 1:2.

Or, y’know, you could just rotate the fuckin’ inside square, which makes it visually obvious.