9th grade – Welcome to infinitefreetime dot com

Every time my kids took a test last year, I went into a depression spiral, because for some reason my test results were consistently worse than all of the other middle school math teachers in my district. My 8th graders took their first real test of the year on Wednesday. And … well.

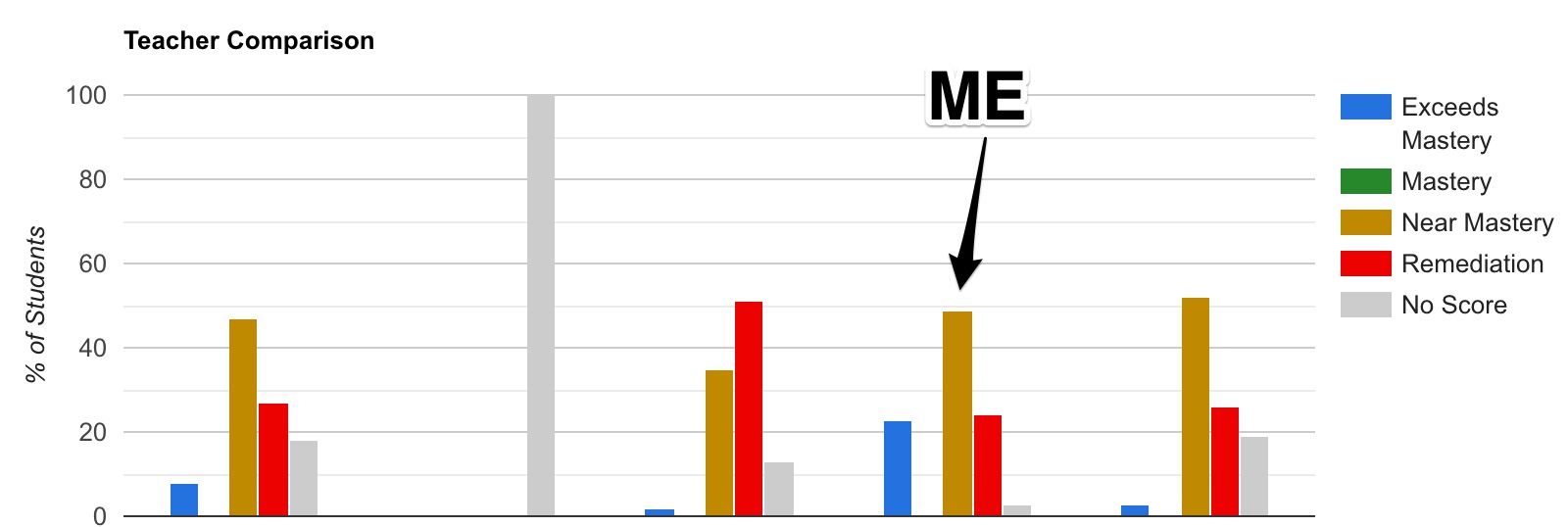
Blue bar is best bar, there’s no green bars for anybody because the idiot person who put the test together forgot to set a level for Mastery, and red is Bad, and white is untested kids. The person who has 100% of his kids mysteriously untested is also the guy who wrote the test and screwed up the scoring. He also set the schedule for when we were supposed to test! And just … didn’t.

But my blue bar is way bigger than anybody else’s blue bar, including Mr. I Work At the Honors School to my right, and my red bar is smaller than everyone else’s, so suck it.

Can we talk about Algebra’s last test? Sure, let’s, and be aware that this is what both of their tests look like:

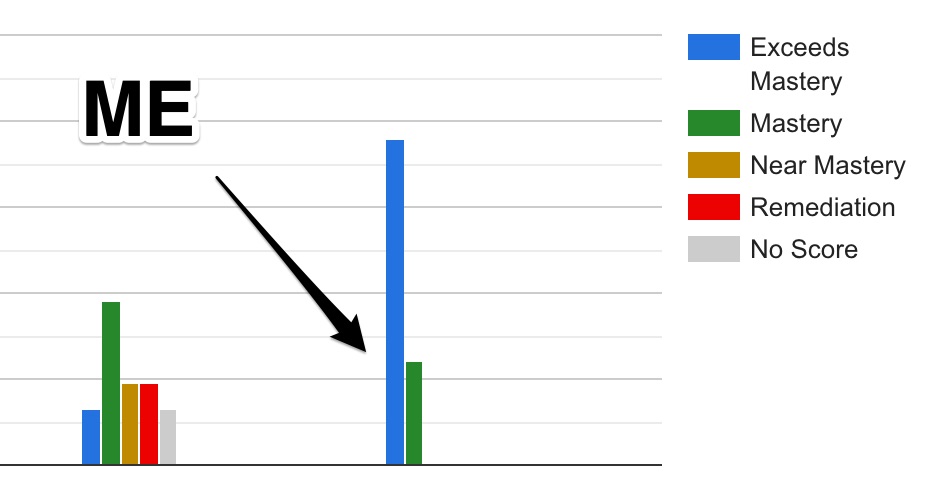
The other teacher is the other Algebra teacher at my school, and yes, I’m still mad that I don’t have both Algebra classes any more, and the reason there are only two is that for some reason the high school teachers aren’t using the system that we’re all supposed to use to keep track of student achievement on the tests the high school teachers wrote.

There’s some inside baseball going on here, obviously, and I’m sorry if this is a little incoherent, but I’m really frustrated with the way this system for common assessments is getting implemented at basically every building other than mine. But y’all know how competitive I am and my kids are kicking names and taking ass so far this year. Which is a fucking relief, after last year.

Oh, and grade-wise? Currently I have one hundred and seventy-four students in my six classes (Algebra has 21, and all of my 8th grade classes but one have 31. My “small” 8th grade class has 29.) and of those 174 kids, only 39 (22%) have Ds or Fs. Considering that last year this happened at the beginning of the third quarter I will absolutely take those numbers. I have way more kids getting As than getting Ds or Fs. That hasn’t happened very often.

So yeah. I’m going to enjoy pretending I’m good at my job tonight.

I have removed the Second Skin from my new tattoo, and the itching is absolutely maddening, so I’m going to distract myself with math. Because that’s why you come here, right? As a reminder, this is the original image, and the question is the ratio of the inner square to the outer square:

The first thing we’re going to do is draw the two diagonals of the inner square. These are, by definition, perpendicular to each other, and they are also equal to the circumference of the circle. Let us define the radius of the circle as x:

What we have now is four right triangles inscribed inside the circle. Pythagoras tells us that the sum of the squares of the two legs are equal to the square of the hypotenuse, which is the line on the left of the square there. Therefore, defining the hypotenuse as Y, we get:

x² + x² = y²
2x² = y²

Take the square roots of each side, and we get:

√(2x²) = √(y²)

And therefore:

√(2x²) = y

Which means that all four sides of the inner circle are equal to √(2x²), thusly:

To get the area of the inner square, all we have to do is multiply √(2x²) by √(2x²), which, conveniently, just gets rid of the square root symbols. The area of the inner circle is 2x².

Now, we need to realize that since the radius of the circle is x, the diameter of the circle is 2x, and that the diameter of the circle also equals the width and the height of the outside square. So that outer square is 2x high and 2x wide:

Therefore, all we have to do to get the area of the outside square is multiply 2x by 2x, which gives us 4x². Which, conveniently, is exactly twice the area of the inner square, which was 2x².

The outside square is therefore twice the size of the inner square, and the ratio of the inner square to the outer square is 1:2.

Or, y’know, you could just rotate the fuckin’ inside square, which makes it visually obvious.